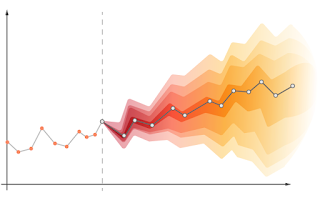
Forecasting with uncertainty
PETER WHITTLE DEVELOPED MANY OF THE STATISTICAL TECHNIQUES later POPULARISED BY BOX AND JENKINS. THEN EVERYBODY REALIZED THE IMPACT OF INTERVENTIONS CAUSING DISCONTINOUS CHANGE.
THIS MAKES IT VERY DIFFICULT TO FORECAST AT ALL e.g. DURING THE
COVID PANDEMIC.
Peter Whittle (1927-2021)
TIME SERIES An Overview and Brief History (Aileen Nielsen)
HIGHLY RECOMMENDED READING
BRIEF HISTORY (Stockholm University)
BRIEF HISTORY AND FUTURE RESEARCH (Ruey Tsai)
The filtering method is named for Hungarian émigré Rudolf E. Kálmán, although Thorvald Nicolai Thiele[13][14] and Peter Swerling developed a similar algorithm earlier. Richard S. Bucy of the Johns Hopkins Applied Physics Laboratory contributed to the theory, causing it to be known sometimes as Kalman–Bucy filtering. Stanley F. Schmidt is generally credited with developing the first implementation of a Kalman filter. He realized that the filter could be divided into two distinct parts, with one part for time periods between sensor outputs and another part for incorporating measurements.[15] It was during a visit by Kálmán to the NASA Ames Research Center that Schmidt saw the applicability of Kálmán's ideas to the nonlinear problem of trajectory estimation for the Apollo program resulting in its incorporation in the Apollo navigation computer. This Kalman filtering was first described and developed partially in technical papers by Swerling (1958), Kalman (1960) and Kalman and Bucy (1961).
Rudolf Kalman (1930-2016)
Helped get rockets to the moon
Kalman filters have been vital in the implementation of the navigation systems of U.S. Navy nuclear ballistic missile submarines, and in the guidance and navigation systems of cruise missiles such as the U.S. Navy's Tomahawk missile and the U.S. Air Force's Air Launched Cruise Missile. They are also used in the guidance and navigation systems of reusable launch vehicles and the attitude control and navigation systems of spacecraft which dock at the International Space Station.[16]
In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck
Leonard Ornstein
COX PROCESSES When the data are simply points in time,
DETECTING DEPLETIONS IN THE OZONE LAYER (By Greg Reinsel et al)
Detected change in trend using time series model
!n the study of detection of a possible change in linear trend at a known time t = T0, as an extension of the statistical model in (1), we consider a piecewise linear trend model of the form

WHITTLE (!953) THE ANALYSIS OF MULTIPLE TIME SERIES
During the 1940s and 1950s the subject of statistical time series analysis matured from a scattered collection of methods into formal branch of statistics. Much of the mathematical groundwork was laid down and many of the practical methods were developed during this period. The foundations of the field were developed by individuals whose names are familiar to most statisticians: Yule, Wold, Wiener, and Kolmogorov. Interestingly, many of the methodological techniques that originated 40 to 50 years ago still play a principal role in modern time-series analysis. A key participant in this golden-age of time-series analysis was Peter Whittle
PETER WHITTLE DEVELOPED MANY OF THE STATISTICAL TECHNIQUES LATER PURLOINED AND POPULARISED BY BOX AND JENKINS AND THEIR MULTITUDINOUS FOLLOWERS. THEN EVERYBODY REALIZED THE IMPACT OF INTERVENTIONS CAUSING DISCONTINOUS CHANGE, AND MANY RESEARCHERS ON THE BANDWAGON SWITCHED TO PATTERN RECOGNITION.
In 1931 Kolmogorov's paper "Analytical methods in probability theory" appeared, in which he laid the foundations for the modern theory of Markov processes. According to Gnedenko: "In the history of probability theory it is difficult to find other works that changed the established points of view and basic trends in research work in such a decisive way. In fact, this work could be considered as the beginning of a new stage in the development of the whole theory".
The theory had a few forerunners: A.A. Markov, H. Poincare and Bachelier, Fokker, Planck, Smolukhovski and Chapman. Their particular equations for individual problems in physics, informally obtained, followed as special cases in Kolmogorov's theory. A long series of subsequent publications followed, by Kolmogorov and his followers, among which a paper by Kolmogorov dealing with one of the basic problems of mathematical statistics, where he introduces his famous criterion (Kolmogorov's test) for using the empirical distribution function of observed random variables to test the validity of an hypothesis about their true distribution. In general Kolmogorov's ideas on probability and statistics have led to numerous theoretic developments, and to numerous applications in present-day physical sciences.
Young Kolmorogov














No comments:
Post a Comment