SPAN OF VECTOR SPACE, AND LINEAR INDEPENDENCE
In the mathematical subfield of linear algebra or more generally functional analysis, the linear span (also called the linear hull) of a set of vectors in a vector space is the intersection of all subspaces containing that set. The linear span of a set of vectors is therefore a vector space.
LINEAR SPAN (WIKI)
This two articles indicate difference between a common sense presentation, and a more obscure pure mathematical presentation. It is important to communicate the essential idea to students before getting into formalism. Many pure mathematicians are much too aloof, toffee-nosed, and confusing to their students.
DOMAIN OF A FUNCTION
To investigate continuity we need a precise definition of the domain, For example, if x=0 is not contained in domain, f (x) may be continuous for all x not equal to zero,
CONTINUOUS FUNCTIONS (WIKI)
In my own words f(x) is continuous at point x if
Limit as Epsilon tends to zero of f (x+ Epsilon) exists and is equal to f (x)
This is a simplification of Weierstrass definition. f is a continuous function if f(x) is continuous for all points x in the domain
EXAMPLES OF CONTINUOUS FUNCTIONS
MORE EXAMPLES
Function f is said to be continuous on an interval I if f is continuous at each point x in I. Here is a list of some well-known facts related to continuity :
- 1. The SUM of continuous functions is continuous.
2. The DIFFERENCE of continuous functions is continuous.
3. The PRODUCT of continuous functions is continuous.
4. The QUOTIENT of continuous functions is continuous at all points x where the DENOMINATOR IS NOT ZERO.
5. The FUNCTIONAL COMPOSITION of continuous functions is continuous at all points x where the composition is properly defined.
6. Any polynomial is continuous for all values of x.
7. Function ex and trigonometry functions
In addition to polynomials, the following functions also are continuous at every value in their domains.
Rational functions
Root functions
Trigonometric functions
Inverse trigonometric functions
Logarithmic functions
Exponential functions
These are the functions that one encounters throughout calculus
Continuity and limit[edit]
Until the second part of 19th century, only continuous functions were considered by mathematicians. At that time, the notion of continuity was elaborated for the functions of one or several real variables a rather long time before the formal definition of a topological space and a continuous map between topological spaces. As continuous functions of several real variables are ubiquitous in mathematics, it is worth to define this notion without reference to the general notion of continuous maps between topological space.
For defining the continuity, it is useful to consider the distance function of ℝn, which is an everywhere defined function of 2n real variables:
A function f is continuous at a point a = (a1, ..., an) which is interior to its domain, if, for every positive real number ε, there is a positive real number φ such that |f(x) − f(a)| < εfor all x such that d(x a) < φ. In other words, φ may be chosen small enough for having the image by f of the ball of radius φ centered at a contained in the interval of length 2εcentered at f(a). A function is continuous if it is continuous at every point of its domain.
If a function is continuous at f(a), then all the univariate functions, that are obtained by fixing all the variables xi but one at the value ai, are continuous at f(a). The converse is false; this means that all these univariate functions may be continuous for a function that is not continuous at f(a). For an example, let us consider the function f such thatf(0, 0) = 0, and is otherwise defined by
The functions x ↦ f(x, 0) and y ↦ f(0, y) are both constant and equal to zero, and are therefore continuous. The function f is not continuous at (0, 0), because, if ε < 1/2 andy = x2 ≠ 0, we have f(x, y) = 1/2, even if |x| is very small. Although not continuous, this function has the further property that all the univariate functions obtained by restricting it to a line passing through (0, 0) are also continuous. In fact, we have
for λ ≠ 0. The limit of a real-valued function of several real variables is as follows.[1] Let a = (a1, a2, ..., an) be a point in topological closure of the domain X of the function f. The function, f has a limit L when x tends toward a, denoted
if the following condition is satisfied: For every positive real number ε > 0, there is a positive real number δ > 0 such that
for all x in the domain such that
If the limit exists, it is unique. If a is in the interior of the domain, the limit exists if and only if the function is continuous at a. In this case, we have
When a is in the boundary of the domain of f, and if f has a limit at a, the latter formula allows to "extend by continuity" the domain of f to a.
EASIER EXPOSITION





Limits
The following definition and results can be easily generalized to functions of more than two variables. Let f be a function of two variables that is defined in some circular region around (x_0,y_0). The limit of f as x approaches (x_0,y_0) equals L if and only if for every epsilon>0 there exists a delta>0 such that f satisfies
whenever the distance between (x,y) and (x_0,y_0) satisfies
We will of course use the natural notation
when the limit exists. The usual properties of limits hold for functions of two variables: If the following hypotheses hold:
and if c is any real number, then we have the results:
- Linearity 1:

- Linearity 2:

- Products of functions:

- Quotients of functions:

(provided L is non-zero)
The linearity and product results can of course be generalized to any finite number of functions:
- The limit of a sum of functions is the sum of the limits of the functions.
- The limit of a product of functions is the product of the limits of the functions.
It is important to remember that the limit of each individual function must exist before any of these results can be applied.
Example
Find the limit of the function f(x,y)=x^3+2yx^2 as (x,y) approaches (1,2). Since the limits of the functions x^3, x^2, and y all exist, we may apply the linearity and product properties of limits to get
Example
The product property of limits cannot be applied to the function f(x,y)=xlog(y) as (x,y) approaches (0,0) since the log function approaches minus infinity as y approaches zero. L'Hopital's rules must be used for this type of problem.
With functions of a single variable, if the limits of a function f as x approached a point c from the left and right directions differed, then the function was found to not have a limit at that point. The same is true for functions of two variables, but now there are an infinite number of directions to choose from rather than just two. Consider the function xy/(x^2+y^2). As (x,y) approaches (0,0) along the x-axis (y=0), the function has limit 0; but, as (x,y) approaches (0,0) along the line y=x, the function has limit 1/2. Thus, the function f does not have a limit as (x,y) approaches (0,0).
A function f of two variables is continuous at a point (x_0,y_0) if
- f(x_0,y_0) is defined
 exists
exists
This definition is a direct generalization of the concept of continuity of functions of one variable. The three requirements ensure that f does not oscillate wildly near the point, does not become infinite at the point, or have a jump discontinuity at the point. These are all familiar properties of continuous functions. As with functions of one variable, functions of two or more variables are continuous on an interval if they are continuous at each point in the interval.
Continuous functions of two variables satisfy all of the usual properties familiar from single variable calculus:
- The sum of a finite number of continuous functions is a continuous function.
- The product of a finite number of continuous functions is a continuous function.
- The quotient of two continuous functions is a continuous function wherever the denominator is non-zero.
Example
The functions sin(xy), x^2y^3+ln(x+y), and exp(3xy) are all continuous functions on the xy-plane, whereas the function 1/xy is continuous everywhere except the point (0,0).
VECTOR PRODUCT
VECTOR PRODUCT
The cross product of two vectors a and b is defined only in three-dimensional space and is denoted by a × b. In physics, sometimes the notation a ∧ b is used,[2] though this is avoided in mathematics to avoid confusion with the exterior product.
The cross product a × b is defined as a vector c that is perpendicular to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.
where θ is the angle between a and b in the plane containing them (hence, it is between 0° and 180°), ‖a‖ and ‖b‖ are the magnitudes of vectors a and b, and n is a unit vector perpendicular to the plane containing a and b in the direction given by the right-hand rule (illustrated). If the vectors a and b are parallel (i.e., the angle θ between them is either 0° or 180°), by the above formula, the cross product of a and b is the zero vector 0.

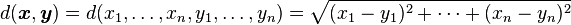



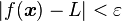



It is a nice post but too big to understand please to to split it..
ReplyDeleteIf you are not getting the detailed information on this blog.. Then boy you can use limit solver as an alternate to sort out your problems.
ReplyDelete